what is Binary Search?

Binary Search

Binary search is the search technique which works efficiently on the sorted lists. Hence, in order to search an element into some list by using binary search technique, we must ensure that the list is sorted.

Binary search follows divide and conquer approach in which, the list is divided into two halves and the item is compared with the middle element of the list. If the match is found then, the location of middle element is returned otherwise, we search into either of the halves depending upon the result produced through the match.

Binary search algorithm is given below.

BINARY_SEARCH(A, lower_bound, upper_bound, VAL)

• Step 1: [INITIALIZE] SET BEG = lower_bound
  END = upper_bound, POS = - 1
• Step 2: Repeat Steps 3 and 4 while BEG <=END
• Step 3: SET MID = (BEG + END)/2
• Step 4: IF A[MID] = VAL
  SET POS = MID
  PRINT POS
  Go to Step 6
  ELSE IF A[MID] > VAL
  SET END = MID - 1
  ELSE
  SET BEG = MID + 1
  [END OF IF]
  [END OF LOOP]
• Step 5: IF POS = -1
  PRINT "VALUE IS NOT PRESENT IN THE ARRAY"
  [END OF IF]
• Step 6: EXIT

Complexity

SN	Performance	Complexity
1	Worst case	O(log n)
2	Best case	O(1)
3	Average Case	O(log n)
4	Worst case space complexity	O(1)

Example

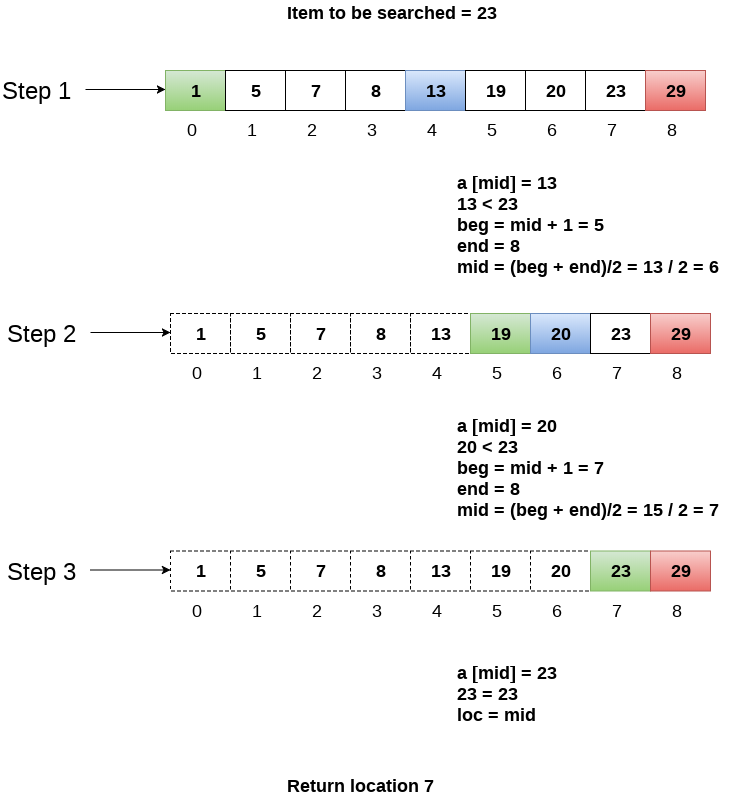
Let us consider an array arr = {1, 5, 7, 8, 13, 19, 20, 23, 29}. Find the location of the item 23 in the array.

In 1^st step :

1. BEG = 0   
2. END = 8ron  
3. MID = 4   
4. a[mid] = a[4] = 13 < 23, therefore  

in Second step:

1. Beg = mid +1 = 5   
2. End = 8  
3. mid = 13/2 = 6    
4. a[mid] = a[6] = 20 < 23, therefore;   

in third step:

1. beg = mid + 1 = 7   
2. End = 8   
3. mid = 15/2 = 7  
4. a[mid] = a[7]   
5.  a[7] = 23 = item;   
6. therefore, set location = mid;   
7. The location of the item will be 7.   

 

Binary Search Program using Recursion

C program

1. #include<stdio.h>  
2. int binarySearch(int[], int, int, int);  
3. void main ()  
4. {  
5.     int arr[10] = {16, 19, 20, 23, 45, 56, 78, 90, 96, 100};  
6.     int item, location=-1;   
7.     printf("Enter the item which you want to search ");  
8.     scanf("%d",&item);  
9.     location = binarySearch(arr, 0, 9, item);  
10.     if(location != -1)   
11.     {  
12.         printf("Item found at location %d",location);  
13.     }  
14.     else  
15.     {  
16.         printf("Item not found");  
17.     }  
18. }   
19. int binarySearch(int a[], int beg, int end, int item)  
20. {  
21.     int mid;  
22.     if(end >= beg)   
23.     {     
24.         mid = (beg + end)/2;  
25.         if(a[mid] == item)  
26.         {  
27.             return mid+1;  
28.         }  
29.         else if(a[mid] < item)   
30.         {  
31.             return binarySearch(a,mid+1,end,item);  
32.         }  
33.         else   
34.         {  
35.             return binarySearch(a,beg,mid-1,item);  
36.         }  
37.       
38.     }  
39.     return -1;   
40. }  

Output:

Enter the item which you want to search 
19 
Item found at location 2

Java

1. import java.util.*;  
2. public class BinarySearch {  
3. public static void main(String[] args) {  
4.     int[] arr = {16, 19, 20, 23, 45, 56, 78, 90, 96, 100};  
5.     int item, location = -1;  
6.     System.out.println("Enter the item which you want to search");  
7.     Scanner sc = new Scanner(System.in);  
8.     item = sc.nextInt();  
9.     location = binarySearch(arr,0,9,item);  
10.     if(location != -1)  
11.     System.out.println("the location of the item is "+location);  
12.     else   
13.         System.out.println("Item not found");  
14.     }  
15. public static int binarySearch(int[] a, int beg, int end, int item)  
16. {  
17.     int mid;  
18.     if(end >= beg)   
19.     {     
20.         mid = (beg + end)/2;  
21.         if(a[mid] == item)  
22.         {  
23.             return mid+1;  
24.         }  
25.         else if(a[mid] < item)   
26.         {  
27.             return binarySearch(a,mid+1,end,item);  
28.         }  
29.         else   
30.         {  
31.             return binarySearch(a,beg,mid-1,item);  
32.         }  
33.       
34.     }  
35.     return -1;   
36. }  
37. }  

Output:

Enter the item which you want to search 
45 
the location of the item is 5 

C#

1. using System;  
2.                   
3. public class LinearSearch  
4. {  
5.     public static void Main()  
6.     {  
7.     int[] arr = {16, 19, 20, 23, 45, 56, 78, 90, 96, 100};  
8.     int location=-1;   
9.     Console.WriteLine("Enter the item which you want to search ");  
10.     int item = Convert.ToInt32(Console.ReadLine());  
11.     location = binarySearch(arr, 0, 9, item);  
12.     if(location != -1)   
13.     {  
14.         Console.WriteLine("Item found at location "+ location);  
15.     }  
16.     else  
17.     {  
18.         Console.WriteLine("Item not found");  
19.     }  
20. }   
21. public static int binarySearch(int[] a, int beg, int end, int item)  
22. {  
23.     int mid;  
24.     if(end >= beg)   
25.     {     
26.         mid = (beg + end)/2;  
27.         if(a[mid] == item)  
28.         {  
29.             return mid+1;  
30.         }  
31.         else if(a[mid] < item)   
32.         {  
33.             return binarySearch(a,mid+1,end,item);  
34.         }  
35.         else   
36.         {  
37.             return binarySearch(a,beg,mid-1,item);  
38.         }  
39.       
40.     }  
41.     return -1;   
42.   
43.     }  
44. }  

Output:

Enter the item which you want to search 
20 
Item found at location 3

Python

1. def binarySearch(arr,beg,end,item):  
2.     if end >= beg:  
3.         mid = int((beg+end)/2)  
4.         if arr[mid] == item :  
5.             return mid+1  
6.         elif arr[mid] < item :   
7.             return binarySearch(arr,mid+1,end,item)  
8.         else:   
9.             return binarySearch(arr,beg,mid-1,item)  
10.     return -1  
11.       
12.   
13. arr=[16, 19, 20, 23, 45, 56, 78, 90, 96, 100];  
14. item = int(input("Enter the item which you want to search ?"))  
15. location = -1;   
16. location = binarySearch(arr,0,9,item);  
17. if location != -1:   
18.     print("Item found at location %d" %(location))  
19. else:   
20.     print("Item not found")  

Output:

Enter the item which you want to search ? 
96 
Item found at location 9 

Enter the item which you want to search ? 
101 
Item not found

Binary Search function using Iteration

1. int binarySearch(int a[], int beg, int end, int item)  
2. {  
3.     int mid;  
4.     while(end >= beg)   
5.     {     
6.         mid = (beg + end)/2;  
7.         if(a[mid] == item)  
8.         {  
9.             return mid+1;  
10.         }  
11.         else if(a[mid] < item)   
12.         {  
13.             beg = mid + 1;  
14.         }  
15.         else   
16.         {  
17.             end = mid - 1;   
18.         }  
19.       
20.     }  
21.     return -1;   
22. }