Explain Array representation of Queue?

Array representation of Queue

We can easily represent queue by using linear arrays. There are two variables i.e. front and rear, that are implemented in the case of every queue. Front and rear variables point to the position from where insertions and deletions are performed in a queue. Initially, the value of front and queue is -1 which represents an empty queue. Array representation of a queue containing 5 elements along with the respective values of front and rear, is shown in the following figure.

 

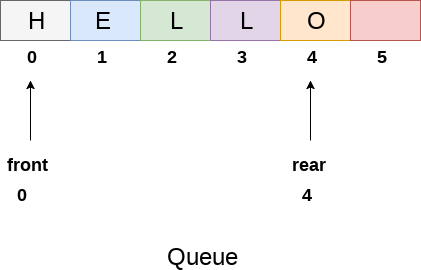
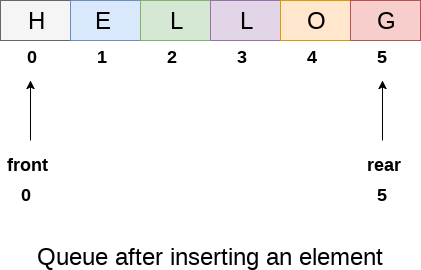
The above figure shows the queue of characters forming the English word "HELLO". Since, No deletion is performed in the queue till now, therefore the value of front remains -1 . However, the value of rear increases by one every time an insertion is performed in the queue. After inserting an element into the queue shown in the above figure, the queue will look something like following. The value of rear will become 5 while the value of front remains same.

 

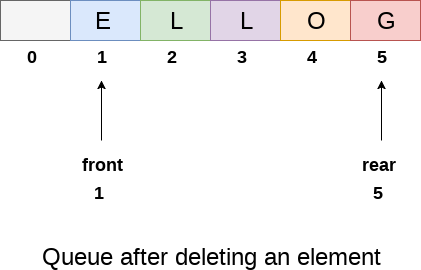
After deleting an element, the value of front will increase from -1 to 0. however, the queue will look something like following.

 

Algorithm to insert any element in a queue

Check if the queue is already full by comparing rear to max - 1. if so, then return an overflow error.

If the item is to be inserted as the first element in the list, in that case set the value of front and rear to 0 and insert the element at the rear end.

Otherwise keep increasing the value of rear and insert each element one by one having rear as the index.

Algorithm

• Step 1: IF REAR = MAX - 1
  Write OVERFLOW
  Go to step
  [END OF IF]
• Step 2: IF FRONT = -1 and REAR = -1
  SET FRONT = REAR = 0
  ELSE
  SET REAR = REAR + 1
  [END OF IF]
• Step 3: Set QUEUE[REAR] = NUM
• Step 4: EXIT

C Function

1. void insert (int queue[], int max, int front, int rear, int item)   
2. {  
3.     if (rear + 1 == max)  
4.     {  
5.         printf("overflow");  
6.     }  
7.     else  
8.     {  
9.         if(front == -1 && rear == -1)  
10.         {  
11.             front = 0;  
12.             rear = 0;  
13.         }  
14.         else  
15.         {  
16.             rear = rear + 1;   
17.         }  
18.         queue[rear]=item;  
19.     }  
20. }  

Algorithm to delete an element from the queue

If, the value of front is -1 or value of front is greater than rear , write an underflow message and exit.

Otherwise, keep increasing the value of front and return the item stored at the front end of the queue at each time.

Algorithm

• Step 1: IF FRONT = -1 or FRONT > REAR
  Write UNDERFLOW
  ELSE
  SET VAL = QUEUE[FRONT]
  SET FRONT = FRONT + 1
  [END OF IF]
• Step 2: EXIT

C Function

1. int delete (int queue[], int max, int front, int rear)  
2. {  
3.     int y;   
4.     if (front == -1 || front > rear)   
5.    
6.     {  
7.         printf("underflow");  
8.     }  
9.     else   
10.     {  
11.         y = queue[front];  
12.         if(front == rear)  
13.         {  
14.             front = rear = -1;  
15.             else   
16.             front = front + 1;   
17.           
18.         }  
19.         return y;  
20.     }  
21. }   

Menu driven program to implement queue using array

1. #include<stdio.h>   
2. #include<stdlib.h>  
3. #define maxsize 5  
4. void insert();  
5. void delete();  
6. void display();  
7. int front = -1, rear = -1;  
8. int queue[maxsize];  
9. void main ()  
10. {  
11.     int choice;   
12.     while(choice != 4)   
13.     {     
14.         printf("\n*************************Main Menu*****************************\n");  
15.         printf("\n=================================================================\n");  
16.         printf("\n1.insert an element\n2.Delete an element\n3.Display the queue\n4.Exit\n");  
17.         printf("\nEnter your choice ?");  
18.         scanf("%d",&choice);  
19.         switch(choice)  
20.         {  
21.             case 1:  
22.             insert();  
23.             break;  
24.             case 2:  
25.             delete();  
26.             break;  
27.             case 3:  
28.             display();  
29.             break;  
30.             case 4:  
31.             exit(0);  
32.             break;  
33.             default:   
34.             printf("\nEnter valid choice??\n");  
35.         }  
36.     }  
37. }  
38. void insert()  
39. {  
40.     int item;  
41.     printf("\nEnter the element\n");  
42.     scanf("\n%d",&item);      
43.     if(rear == maxsize-1)  
44.     {  
45.         printf("\nOVERFLOW\n");  
46.         return;  
47.     }  
48.     if(front == -1 && rear == -1)  
49.     {  
50.         front = 0;  
51.         rear = 0;  
52.     }  
53.     else   
54.     {  
55.         rear = rear+1;  
56.     }  
57.     queue[rear] = item;  
58.     printf("\nValue inserted ");  
59.       
60. }  
61. void delete()  
62. {  
63.     int item;   
64.     if (front == -1 || front > rear)  
65.     {  
66.         printf("\nUNDERFLOW\n");  
67.         return;  
68.               
69.     }  
70.     else  
71.     {  
72.         item = queue[front];  
73.         if(front == rear)  
74.         {  
75.             front = -1;  
76.             rear = -1 ;  
77.         }  
78.         else   
79.         {  
80.             front = front + 1;  
81.         }  
82.         printf("\nvalue deleted ");  
83.     }  
84.       
85.       
86. }  
87.       
88. void display()  
89. {  
90.     int i;  
91.     if(rear == -1)  
92.     {  
93.         printf("\nEmpty queue\n");  
94.     }  
95.     else  
96.     {   printf("\nprinting values .....\n");  
97.         for(i=front;i<=rear;i++)  
98.         {  
99.             printf("\n%d\n",queue[i]);  
100.         }     
101.     }  
102. }  

Output:

*************Main Menu**************

==============================================

1.insert an element
2.Delete an element
3.Display the queue
4.Exit

Enter your choice ?1

Enter the element
123

Value inserted 

*************Main Menu**************

==============================================

1.insert an element
2.Delete an element
3.Display the queue
4.Exit

Enter your choice ?1

Enter the element
90

Value inserted 

*************Main Menu**************

===================================

1.insert an element
2.Delete an element
3.Display the queue
4.Exit

Enter your choice ?2

value deleted 

*************Main Menu**************
==============================================

1.insert an element
2.Delete an element
3.Display the queue
4.Exit

Enter your choice ?3

printing values .....

90

*************Main Menu**************

==============================================

1.insert an element
2.Delete an element
3.Display the queue
4.Exit

Enter your choice ?4

Drawback of array implementation

Although, the technique of creating a queue is easy, but there are some drawbacks of using this technique to implement a queue.

• Memory wastage : The space of the array, which is used to store queue elements, can never be reused to store the elements of that queue because the elements can only be inserted at front end and the value of front might be so high so that, all the space before that, can never be filled.

 

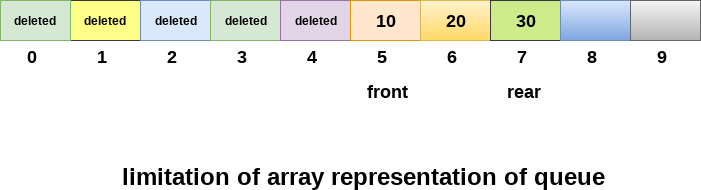
The above figure shows how the memory space is wasted in the array representation of queue. In the above figure, a queue of size 10 having 3 elements, is shown. The value of the front variable is 5, therefore, we can not reinsert the values in the place of already deleted element before the position of front. That much space of the array is wasted and can not be used in the future (for this queue).

• Deciding the array size

On of the most common problem with array implementation is the size of the array which requires to be declared in advance. Due to the fact that, the queue can be extended at runtime depending upon the problem, the extension in the array size is a time taking process and almost impossible to be performed at runtime since a lot of reallocations take place. Due to this reason, we can declare the array large enough so that we can store queue elements as enough as possible but the main problem with this declaration is that, most of the array slots (nearly half) can never be reused. It will again lead to memory wastage.